Tilps Page |
Affine Geometrie / Affinitäten |
 |
Verkettung zweier Achsenaffinitäten
Hier sind mehrere DynaGeo-Fenster untereinander angeordnet. In Fenster 1 ist zusätzlich das Koordinaternsystem eingeblendet. Sa ist das Bild der Ur-Kirchturmspitze, a=A1A2 die zugehörige Achse. Sb ist das Bild von Sa und b=B1B2 deren zugehörige Achse. Die Affinitätsstrahlen sind grün. Bewegen Sie der Reihe nach vorsichtig (im Wechsel) die Punkte A1, A2, B1, B2 und Sa, Sb um wenige Zentimeter; orientieren Sie sich dabei an den Gitternetzlinien. Beobachten Sie, wie sich die Bilder dabei verändern, aber entsprechende Affinitätsstrahlen parallel bleiben.
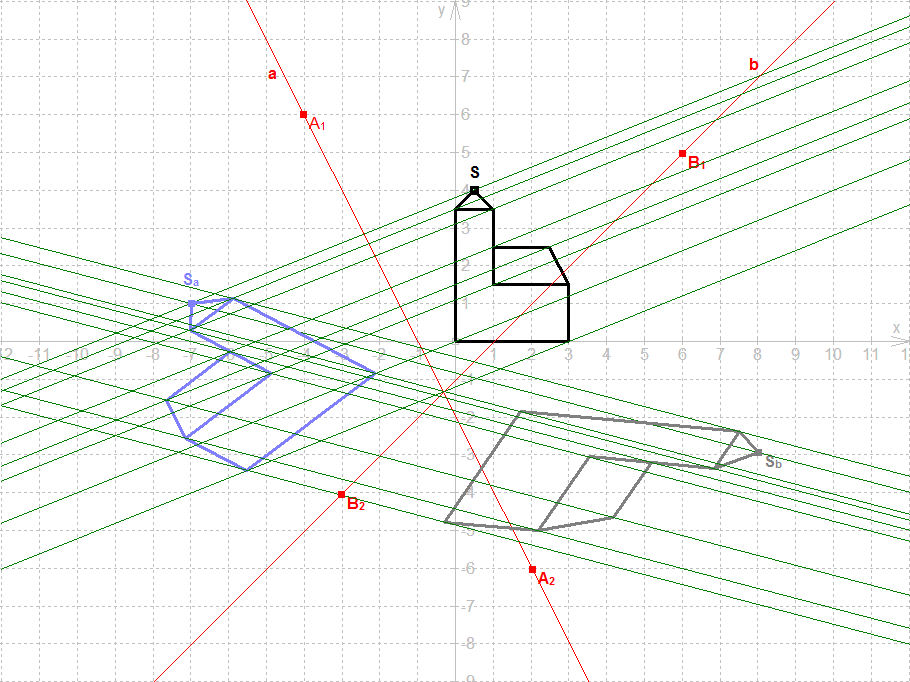
Fenster 1
In den folgenden Fenstern ist das Koordinaternsystem wieder ausgeblendet. Ferner sind für jede der beiden gegebenen Achsenaffinitäten nur noch je zwei Affinitätsstrahlen sichtbar.
In Fenster 2 wurde nun zusätzlich die Reihenfolge in der Verkettung vertauscht: die graue Kirche ergibt sich durch die (ursprüngliche) Reihenfolge S→Sa→Sab und die orangefarbene Kirche durch die Reihenfolge S→Sb→Sba. Offensichtlich sind das unterschiedliche Verkettungen, denn die Ergebnisse stimmen nicht überein (die graue und die orangefarbene Kirche haben unterschiedliche Lage und Form). Also ist die Verkettung linearer Abbildungen i.a. nicht kommutativ (in der Reihenfolge der Hintereinanderausführung nicht vertauschbar)!
Versuchen Sie trotzdem, die beiden Kirchen zur Deckung zu bringen.
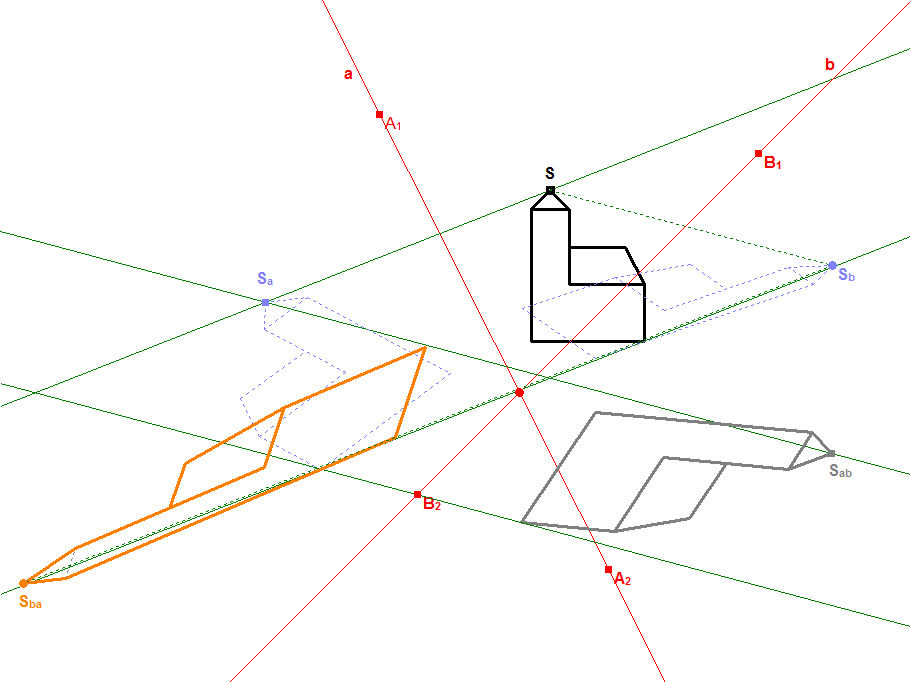
Fenster 2
Falls Sie die eben gestellte Aufgabe nicht geschafft haben sollten, bietet das folgende Fenster 3 die Lösung: Oberhalb der orangefarbenen Kirche ist ein blauer Hilfskreis angegeben und unterhalb der grauen Kirche ist ein grauer Hilfskreis eingezeichnet. Lassen Sie die beiden Achsen ortsfest, bewegen Sie nur Sa in den blauen Kreis und Sab in den grauen Kreis. Justieren Sie wechselweise Sa und Sab. Welche Besonderheit entdecken Sie, nachdem Sie die graue und die orangefarbene Kirche zur Deckung gebracht haben?

Fenster 3
Richtig, die beiden Sorten Affinitätsstrahlen sind parallel zur jeweiligen Achse. Genau, wenn das der Fall ist, wird die Verkettung der beiden (nun speziellen) Achsenaffinitäten kommutativ bezüglich der Hintereinanderausführung und das Ergebnis ist eine Euler-Affinität.
In den folgenden Fenstern ist nur noch die ursprüngliche Verkettung S→Sa→Sb eingezeichnet.
In Fenster 4 sind für jede der beiden gegebenen Achsenaffinitäten jeweils drei Paare Urgerade-Bildgerade grau gestrichelt eingezeichnet, die sich jeweils auf der zugehörigen Achse schneiden (müssen). Lokalisieren Sie die Schnittpunkttripel auf jeder der beiden Achsen (rot eingekringelt). Beobachten Sie deren Bewegung auf der Achse, wenn Sie die Lage der gegebenen Punkte verändern.

Fenster 4
In der folgenden Darstellung 5 ist das blaue Zwischenbild lediglich ausgeblendet; nur noch Sa ist davon sichtbar. Zweifelsfrei handelt es sich bei der grauen Kirche immer noch um das Bild der schwarzen Kirche. Bewegen Sie vorsichtig Sa und beobachten Sie dabei die graue Kirche. Zwischen den beiden Kirchturmspitzen und zwei weiteren Punktepaaren sind helltürkisfarbenen Verbindungsgeraden gezeichnet. Was fällt auf? Ferner sind grau gestrichelt wieder drei Paare Urgerade-Bildgerade samt Schnittpunkten eingezeichnet, diesmal für die Zuordnung schwarz → grau. Was fällt auf?

Fenster 5
Offensichtlich besteht zwischen der schwarzen und der grauen Kirche keine Achenaffinität mehr, denn die grauen Schnittpunkte der drei Paare Urgerade-Bildgerade liegen nicht auf einer gemeinsamen Geraden und die helltürkisfarbenen Verbindungsgeraden entsprechender Punkte sind nicht mehr parallel. Andererseits sind die Eigenschaften 1 - 3 aus Abschnitt 4 erfüllt, nur Eigenschaft 4 ist verletzt. Die Abbildung schwarz → grau ist also eine Affinität, aber keine Achsenaffinität mehr.
Versuchen Sie nun durch Bewegen von Sa und Sb dafür zu sorgen, dass sich die drei türkisfarbenen Geraden in einem Punkt schneiden.
Eine Lösung könnte sein, Sb nach unten in die Mitte des von den beiden Achsen gebildeten unteren "Quadranten" zu verschieben. Mit etwas Geschick schaffen Sie es vielleicht, dass der Schnittpunkt der drei türkisfarbenen Geraden mit dem Achsenschnittpunkt zusammenfällt. Das wären immerhin fünf Geraden mit einem gemeinsamen Schnittpunkt. Allerdings gibt die Auflösung der Zeichnung keinen hinreichenden Aufschluss der Vermutung. Ist damit trotzdem etwas neues entdeckt?
Wenn Sie die Zeichnung ganz genau betrachten, erkennen Sie die vierte Verbindungsgerade (helltürkis gestrichelt, damit sie nicht gleich auffällt). Und die verläuft leider ohne die gewünschte Koinzidenz.
Eine andere Lösung ergibt sich analog zu Fenster 3. Wenn Sie nämlich durch zusätzliches Bewegen von Sa dafür sorgen, dass auch die "störende" Verbindungsgerade durch den eben "entdeckten" Schnittpunkt geht, dann sind wundersamerweise die Affinitätsstrahlen parallel zu den entsprechenden Achsen (Euler-Affinität) und die Bildkirche hat eine besondere Form und Lage. Welche?
Dietrich Tilp | 01.2014 | 11.2022